Chapter 4

STRUCTURES.

If I tell you that I could magnetize water you would not be surprised, for we know already that all of nature is formed by systematic arrangements.  To make ice out of water is nothing more complicated than to slow down the molecular motion to such a point where they will grasp a firm hold unto one another, making rigid lines and structures which right before our eyes is water turned into ice.

We place water in our deep freeze for ice cubes by the difference of the temperature, yet we rarely think of this lowering of the temperature as if we were gluing together the molecules, or making them holds hands by their motions one to the other. And even less do we think of it as holding by magnetic force like all other magnetic force only more basic. The reason that we can see and feel a magnetic force in a bar so magnetized and not in water does not take away the fact that there are magnetic motions holding properties. For if indeed we think of magnetism as magnetic properties and that only certain materials have magnetic properties we are still tied to the story that the stork brings babies and Santa Claus lives at the North Pole.  

Certain structure formations are capable of conducting a special formation of motions whole other are not capable thereof. How many figures of two numbers one of which shall be an uneven number can attain unto the number 37? If by this example the value for a structure formation to conduct such a force-lining must be 37 then only such substances as are so arranged to add to that value can conduct it. which we shall learn better later on.

We mentioned something about decreasing the molecular motion of water a moment ago, and to pursue this, this molecular motion is not just the velocity at which molecules fly back and forth in the water, for if it were then the whole body of the water would be the wildest hurricane of water anyone has ever seen in a cup, or drum or whatever.  Just use your reason and consider how molecules are the substance that is water and water is the substance of the molecules, and a host of molecules lightly holding on to each other is a drop of water. If therefore the molecules are to fly back and forth rapidly what do you imagine we would see? They do vibrate however and move about.

But now I mentioned two things because the moving about is not directly from the molecular motion itself, but from differences in the temperature stirring currents or flows of water from place to place, seeking a natural balance. But to vibrate, yes, that is part of it, but by no means the primary motion that makes for the temperature of things. If for example we see water boil and it is jumping all over, that also is not because the vibration is so great that the water moves, but it is only the pressures of warmer molecules, versus those of colder molecules, against the forces of gravity. Equalize the temperatures and the water will no longer boil.

The primary mover in temperature is velocity still, the velocity of the particles as they move in place. And make no mistake about it, within such a great system these velocities are critical to their structure formations. By it, they expand in size and rearrange themselves just as water to ice is a good example thereof, and variations of this velocity are felt by every creature as either hot or cold to them as they judge it by the average medium that is common to them.  

Usually I call heat the average motion of the substance, so that I might usefully include velocity, vibrations, and average degree of balance. But the most of these remains to be velocity.

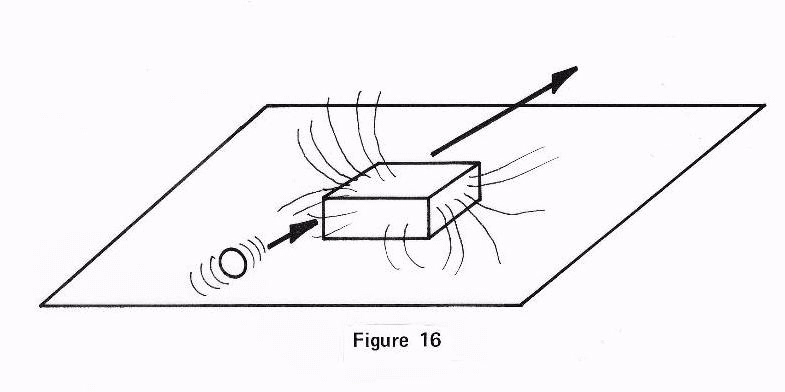
To rightly understand all this, let us place a magnet firmly on a table, as in Figure 16. Then let us pass a steel ball in front of it, so that when it comes in front thereof the magnet pulls and holds it. If then we repeat this little game increasing the velocity of the ball, the magnet will quite soon no longer retain the ball, unable to hold it because of the increased velocity. And a still greater velocity, would not even deflect the motion of the ball in a straight line.  

If therefore you can understand this, you can rightly understand by what principle water becomes ice and butter melts to a liquid; or paper is turned into gases and ashes by a fire; and moreover how the differences of these velocities are in fact and indeed magnetic in their fundamental concept. For at any time when two motions are capable of aligning with each other and holding on to each other, things are bound together. But when they misalign through positioning or by too great a difference of velocity, they may not combine, or even be separated, which depends upon all the circumstances surrounding it.

 

We are of ourselves not quite so capable to plan all these arrangements and to place all these things by their number so that they would have certain values of power to one thing, and other values of power to other things. By and large they form exactly that which we had planned to gain as a net result.

We are not able to even do this with one thing in nature, although we are able to perform some child's play unto nature to put engines together, and construct electronic devices to perform certain functions we planned for it. But things such as our Creator formed by the power of His Word alone is a slight bit over our heads.

Therefore we marvel at the understanding thereof, especially realizing the perfection of it and that in such an endless multitude of variations that we can not easily find two snowflakes alike unto each other.  

To use another example let us take two hydrogen atoms, each of which has one electron and several protons for its base, or sun. And let us take also one oxygen atom with 8 electrons, and presumably 16 protons. These atoms, when they are single and placed into one and the same container, can do all the courting they want and play the love-bait, but no marriage or matrimony shall be concluded unless a feast is given, such as a velocity for a minister. The individual capability or possibility of these atoms is such that no permanent bond can be made between them. If any bond is to made, they must be paired two to one, two of hydrogen to one of oxygen. 

To introduce a spark therefore in such a medium, we introduce a motion or a velocity that is acute and greater than the average velocity of the atoms happily extending nature's general lines of motion (the U/M/F). The instant when such a velocity is thrust upon a number of these atoms, however, they are ; Speeded up, and thrust together in a bond of matrimony. They do not just merely hold on to each other by magnetic forces alone like two ball magnets might, but something more intricate has occurred, which prevented their premature concept of matrimony. They so it is said inter-space each other by their electrons, like a man and woman arm in arm.  

But now that they are paired, immediately they have lost the structure pattern that was theirs in their single state, taking on a new structure pattern, that of water, for H20 is water. And now we can actually see the substance which before was invisible unto us. If we desire to separate these pairs once again, and we gradually increase the average velocity thereof, we shall fail unless we go very high indeed, because the increase of that velocity will merely separate the molecules further from one another creating water vapor instead of the liquid form.

But even in its liquid form, the pairs may be separated if only we apply applicable motions unto it, that will rupture their bond, or a velocity in such a manner as to force them apart. One such is an electric current when conducted through water not too pure, but rightfully the components should follow opposite directions along with the flow of the current to bring up, one on one side and the other on the other side, for if I am not mistaken, I believe we do actually pull them apart by an electric current. Figure 17

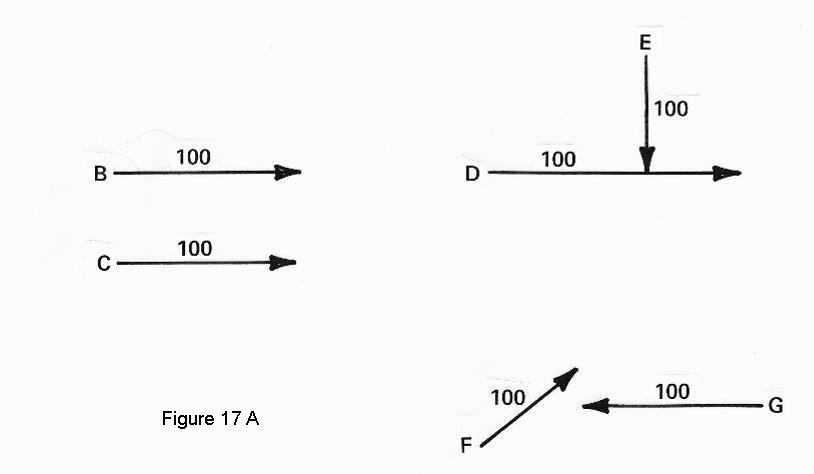
The fundamentals that underlay the formation and bonds of all matter are threefold. They are: velocity, polarity, and coordination. Velocity is the difference between one motion and another by the speed thereof, and/or their angles of direction, including their timing. Let us suppose two motions as in Figure 17-A, each to have a velocity of 100. Both C and B, traveling in an identical direction leaves us with no differential, but when a motion, E, is at right angles to another motion, D, there is a most certain differential, although their re­spective velocities are equal.

    

A collision would divert the paths of the particles so in motion. When they bypass one another but still do contact upon one another by their forces extended from them, their paths will not be changed by the same computations as in a collision. What will occur must be calculated by not only the fact that they are at equal velocity, and at right angles to each other, but their angle of position to each other as they pass by which could result in a number of ways by the number of possibilities that exist.

Our best example is a magnet again. We can experiment with simple magnets to determine these probabilities, and find that they conform with nature, provided we experiment correctly. When we take a motion such as F, relative to motion G, a different differential will be observed. Note therefore how this one word, velocity, embraces much more than it implies, to include directions and powers of motion, and their timing.  

It is logical that a two-pound stone traveling at a velocity of 100 shall not perform the same degree of action which a 20-pound stone at a velocity of 100 shall perform. Then let us suppose two atoms, H and L, to inter-space with each other. When electron K, is where indicated, and the electron M, follows on behind it, as it were to move around the path by electron K, or to follow at the heels thereof, they act upon one another by their relation at a distance, and in accordance with their motions which, being controlled by their respective nuclei, will have a bearing on the atoms themselves, and their relation as a pair.

All this is but one of the fundamental basics of the final outcome of the structures of matter. While our next basic is called polarity, we should realize that we mean their magnetic forces, being again the differences of motion within one entity, but not a difference of velocity. Velocity obeys a two-point principle, and polarity a three-point principle. In a two-point principle, we recognize things by the difference of two, while in a three-point principle, we recognize things by the difference in one, and not in the difference of three.

The third fundamental basic which helps put together all things in nature, from our fingernails to the jewelry we wear and from the leaves of a plant to the air we breathe, is the coordination of structuring itself, and might in a sense be called its mathematics. And to convey this unto you, let us go to some common examples. 

A gasoline engine is a material part, just like the real substance of an atomic particle is a material part. While the motion of the cylinders and shafts, etc., are purely motion, as that motion which is upon these material parts, or of it, we thus conclude with two basics of nature: its matter, and its energy.

Yet shall this engine be of little use unto us, and in fact be not an engine as such, except as it has a firing order, that is to say, except as it has a definite order by which all these parts might function one to the other in a single harmony. It is this part of the engine which we can not touch or lay our hands upon, even as we are unable physically to place motion as a substance of real existence. Yet it exists and performs our moves. We can touch an order only by the former two to change it, but in itself it is mathematical or the very ideal of coordination.  

So likewise with nature, in all of its particles and the motions that are upon it, would not be the nature, except for the coordination of it. If therefore we should think it difficult to know how these particles of nature can follow a coordinate, then I suppose we never have realized much at all about the manner in which plants do grow, or a child is born, or how all things work. For suppose the firing order is out of timing. Then the engine will not run, but corrected it runs again, and shall not likely deviate if properly secured.

We can make nature to ourselves by a similar example, such as to write this very page we require a material part, the paper and the ink, and we require a motion by which to place the contrast black on white. But tell me how shall we be able to portray anything unless first of all we established the very coordination, that is, our language, to begin with, that one certain line shall make for one contrast, and another contrast, unto a final end that displays what is? And all this by these three in one. 

We commonly think that gasoline engines are manufactured at a factory by real people who think them out and place things by their order. But we are mistaken, because they evolve by accident like everything else evolves by accident. A lot of realism that represents to us, yes, but why then shall the kernel of a cell be evolved by accident, like a computer that reads out how the cell must multiply and by what order it must do this? The scientists have discovered this to be so themselves. The computers of these cells, and of any other cell then, are just as accidental as the radios we buy in the store and the cars we drive to work.

We might also visualize the forming of the structures of nature as like unto a woman knitting. If she follows a certain order of motion with her needles and wool, she will knit a shirt, but if the order is wrong, it will fall apart or be a mutation. And if she follows different patterns of orders, she will make different formations of structures. While we can unite things by gluing them together, or by holding hands, we can also weave and make things hold together by that process.  

Shall I now describe every pattern of motion in nature, and define every computer in nature, and precisely lay out all motions and every direction of motion by their value and velocity, and their principle with their timing, etc.? Ah, yes, that would indeed be something, for that would mean a wealth of knowledge and insight that can no longer be compared to that of the rest of us. The smaller insight to understand the principle of the things alone makes child's play out of our current theories.

A substance such as diamond is very hard, while a substance such as sponge rubber is very flexible, both of which are held together by their motion of magnetic and their average velocity and their ideal of coordination to make for a structure of things. And both are visible unto us, and both can be held by the hand, but when we fully separate these structures to leave but the atoms in their individual state, then neither diamond nor sponge rubber is any longer visible, nor can they be held by the hand. What may appear unto us as nothing in one state can therefore become a jewel worn on our finger in an other state after going through the process of formation.  

Think not, however, that we can make diamonds out of the air around us, because our air consists of atoms with only a certain number of electrons, chiefly two certain atoms, and the value to acquire diamonds calls for some atoms with a greater number of electrons in order to promote the ridgidness of the bond it presents. If our air, for example, contained all the necessary ingredients required for a diamond, then by the right order, a diamond may most certainly be made, just the same as one certain pattern of knit may be made by knitting in the order for that.

Now I should think to have well enough represented the manner in which all of nature is borne forth by its components. One thing I wish to mention regarding our eyesight is how it is that we are unable to see things as small as an atom. Our eyes are really but instruments to receive and transmit that which occurs outside of our body to the nerve centers in our brain, where they are related unto us, as we are spiritual be­ings living within a body of substance, and very much associated with it.  

The manner now in which such representations come unto us shall be no different than such things as are the very things represented, meaning nature is matter in motion, and by motion it makes for all things, and again by motion does it represent itself unto us, because it can not perform in any other way, or but do what it is natural to it.

It is by these variations that all things are finally seen by us. Take color for example. When a certain stroke or length hits us, it will be understood as of one color, while a variation to a length shorter or longer will be understood as a different color again. Nature therefore knows not colors, seeing they are only interpretations of our understanding. Nature knows one length from the other, however.

These motions therefore brought to us are by a variation of motion itself, called a vibration, a back-and-forth movement of a line of things, or the position of a particle of the medium in relation to others. It is transmitted unto us at the velocity of light, which might appear very fast unto us. (And it may also depend on what is fast to whom. It could be said, to be slow, also.)

Knowing what light is, and how it might be transposed through a medium, and therewith realizing nature to be the greatest system of highways ever conceived, to know that it is not solid but more like a rubber sponge, we should realize that, while one vibration of light travels down one line of motion over the structure of things and another travels over the next line of motion parallel to it, there can indeed be a most definite spacing between them. And in fact this spacing is so large, in comparison to the size of one atom, that to try and see a single atom by the wavelength of light is like trying to gather water into a fish net.

And just the same as we are able to catch fish in our nets but not the water, so we are able to see things which are large enough to span fully across the width of the waves, since in the same way they can reflect the vibration unto us. To see a atom therefore is really a problem of logistics.

A little later on we shall learn more concerning the lines of motion in nature, and how they are set forth. When then we shall realize how it takes actually the total of quite a number of atoms to set forth but one section of such a line, we should realize even better how one atom can not measure up to a line of motion, and how a line of motion can not come down to size to be equal unto the atom.

We have brought our attention on waves now, and to stay with this for a little more, we should come to realize also how any other wave, such as radio waves or X-rays, or other electro-magnetic waves may be propagated upon the medium which is everywhere, and at some places more dense than at others.

It is true now that all wavelengths of all rates of frequencies are variations of motion, but not all of them are strictly a back-and-forth vibration, such as light is unto us. If we take a rubber band and cut it to have one straight length, and we twist this band a number of times, we also have a variation, for in a straight line we must now go up and down to follow the band if we want to touch it at all times. Or if we desire to follow the band by one of its edges, we must go around in circles at the same time while we move forward along the line thereof.

Thus we have a twist, and we can do two things .with it, one of which is to have power to motivation, simply by connecting something at one end of the band, and while we hold the other end, we let the band un­twist itself making the object at the end thereof move. Or we can transpose a variation of motion by the difference it will make in going to a circle from a straight­forward line.

A rubber band is not the best example for it, because our lines of motion in nature are not physical lines, even though they are made up of physical objects, and as a rule they extend straight on forward, except when forced to turn about. But we must think of this turnabout as a motion in place. And if we conceive within our mind a straight line, at 12 o'clock high to move directly away from us, as we look at the clock in front of us, and then someone pulls with a sudden jerk on that line towards the one, we have a differential that can be measured by still other motions relative to it.

For while the first part is already at 1 o'clock, the rest is still lined up with the 12, but not for long, because the line is all motion seeking uniform balance. Therefore this single jerk will be taken away from us, all down the line. Just the same we can demonstrate to ourselves with any rope or string, and they are yet but idle lines in them­selves.

It is in this manner that radio waves are transmitted, as variations in the lines of motion measured by others. And wavelike, the radio waves are the waves that most closely resemble the waves of an electric current, both being a rotational propagation of motion. To have a radio wave and a light wave simultaneously is quite simple. Even upon one and the same line of motion, neither one will interfere with the other, and both will travel at the same rate of velocity.

As inquisitive humans (if that is what we are?,) we wish yet also to know and understand how in all the criss-cross of motion and lines of motion in nature, there can be straight lines. And moreover how light will travel upon these lines in straight paths even as sound and radio waves do also. For we reason, if light is as I say it is, and we know it travels in straight lines, then nature must have straight lines, and long straight lines at that. But under a microscope, and by sense of reason also, such are hard to see or visualize. But it will be more appropriate for me to come back to this later, and also I must have at least once challenge in this book for my readers.  

Therefore let us consider these things and reason, to return later and compare notes. The problem will actually answer itself, and when we see it we shall find it dead simple, but also a little tricky I might add.

Chapter 5

Magnetic forces.

The first two orders are completed so far, and having thus assembled all things to their form, we require yet but to move the earth in orbit around its sun, and bring forth a motion which may rotate magnets in a circle such as an electric motor. These forces belong to what we call the third magnitude of nature, the last of its orders in the way of things.

We know them by their names: gravity, electrical current, and magnetic force. The one named gravity is not altogether a force belonging to this order, yet we commonly place it there while both the forces of electricity and magnetism are really but one and the same, which are called magnetic force. When we speak of a direct, or linear, magnetic force such are all magnets, we shall name them directional magnetic forces, or plainly magnetic forces, while a rotating, or angular magnetic force, such as all electric currents, is called a rotational magnetic force, or plainly an electric current

Before we into them we should, however, realize what we are getting into. When we spoke of the motion of atoms and molecules to set forth general lines of motion, and magnetic differences by which they act towards one another to make for all things, we said that the motions of cylinders in an engine propel a vehicle upon the road, and so linear motivation is set forth.

What we did not explain is how these cylinders move in relation to each other and the wheels and/or the pavement to produce this ultimate linear motion. In ex­plaining, therefore, the nature of magnets and currents, we are in fact defining an order of things, like the order in which all the parts of the engine move, to make the car move on the road.

It should be obvious that having one car on the road, we need not make a still bigger car out of 10 cars, to really get anywhere. Therefore we require to add nothing unto nature, or multiply its final form, to arrive with greater things. That eventually may be our motion around the sun, and so on. Yet we need greater motion of things, over and beyond those of nature in its natural state.

These are not made out of new things, but they utilize nature's natural motion, simply combining them into certain formations or, we might say, aligning the general motion to overall and greater formations, which consequently can perform greater acts. Such indeed is the secret of electricity as electric current, and magnetism as magnetic force. By these very same motions do all planets and stars revolve and move about in space, with gravity included in them.

Realization now is a most important factor in education, for even though you may know it now by reading, yet has it not come to a much-needed realization yet. For you just heard a secret that many wise men have wondered about over centuries and were unable to pick out and understand, and would have given their right arms for it, while you need but give a few minutes of your time for it.

And to awaken some realization, consider how Newton established the fact that all bodies are held by a force of gravity. He explained not what this gravity was or how it motivates, but he did calculate movements in the sky to correct outcomes. Were I but to state that the planetary motions are by magnetic forces, we can confirm this by all that we already know of a magnet and the solar system, and how irregularities go hand in hand with one another.

And were I a well-known professor, it would be accepted. But being what I am, I would be held a fool. And yet I do say it, and much more, and what is more is not by the cunning of a man, for what the true natures of things are, each of us may know that will know. The foundations of our earth are given for all of us and not me alone.

While thus these foundations are such a single picture with all of nature, and electricity or magnetism, or light or heat or sound are all such very integrated parts. To really know them by their nature, all this I must explain upon its fundamentals, and principle thereof, as far as they concern the third magnitude of nature.

After we have done this; we then want to know also the order, and manner, of the formations that are below this third magnitude and under the surface of nature, to know them also, and better yet, all the way down to the first, order. But that is a very big order, don't forget, and although I am able to explain much of these formations of the first two orders, yet do I not know all of them. As we should realize from our previous chapter, how should one be able to write down the full and complete order of a substance such as silver for example.

First let us understand what force and motions are, and the potential thereof, or motivation. To have a force is to have power for a motion of force. Or it could be moving already, being a force in action. A jet airplane, standing on the runway with its engines at high speed, has quite a potential of force built up, yet it is not placed into action until we activate it so. A force can therefore be one doing work, or being ready for work.

And again, a motion in place must be understood as also being a definite force, capable to do work and promote motivation, just as our jet engine, when firmly secured pulling the air in and blowing it out, is in itself a motion in place, air providing motivation unto something upon it, or through it, which motivation in turn can empower any number of things.

Let us review the basics of some motions and their relations to one another. In Figure 18, let us have a point. A, and let a motion proceed from it which pushed against a plane at B. Shall it be likely now for us to register a push on the plane of B if B were secured, but point A is free to move? The answer is no and yes. For we would register some push, but not the full strength of the motion, because A is free to move, and pushed backwards by the motion as it touches upon the plane, B.  

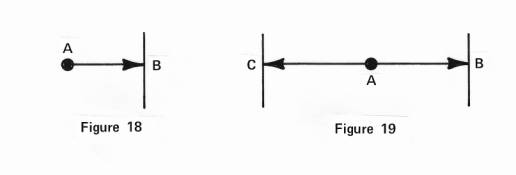
Suppose then in Figure 19, we place another plane, C, on the other side, and add one more motion in the opposite direction. Then the total push against each plane is equal to the strength of any one force, and point A remains in the center. If then we suppose that this point is the engine which brings forth these motions to both directions, where do we suppose the point would reside between these two planes? In its dead center, of course, because they are equal, pushing equally hard on both sides.

Even if the forces are not equal, the point would still remain in dead center, since no one force can present any greater push than that amount of force by which it is backed up, when such are of one entity, or the same engine, balancing each other out. And this is the famous principle of equal actions, or, it is one example thereof.

There is thus a difference in force, and a difference in one thing from another, when we speak of a force of equal actions or to operate by equal actions, because in Figure 18, the action of the motion against the plane will equal the movement of the point in motion as it moves back. This is like a rocket, or an airplane.

But in Figure 19, the point need not go anywhere, and yet can produce full force to the planes. Because it is self-sufficient, self-sustained, and self-balanced, it has its own equal in force, over and upon a point in the center. Such are magnets and electric forces. Suppose in Figure 20 we take a rectangle, and we desire it to have a flow of force within that might give us a power to motivate something on the outside of it.

  

Then let this force of motion be between points A and B, and let the same be placed there by the force, C. Suppose now we pushed inwards against that motion at point B, we would find a resistance, because C is the power and is upholding the line all the way to B, and if we pulled on it, we find again a resistance for the same reasons, because we pull against C.

Then let us suppose we put the line from A to B in the frame, and we withdrew C, and pushed against it at B. Then we would push the line of motion right out of the frame, for nothing is holding it, or we could pull it out. We might at this time reason, "Yes, but the line is secured to the frame. Therefore to push on it would move the frame also."

And you are correct, if indeed the line were secured to the frame, but we did assume it not to be, by our power C, before. Instead we realize this force of motion to be a force not directly of the substance of the frame but a force drawn upon it utilizing the movements of the substance by a formation of alignment.

Therefore when it has aligned these motions once and is somehow secured to the frame, or secured to the motions of the substance of the frame, then a-push against it would move the frame also. But this line of a single alignment drawn over it would roll right back out over the movement of the motion of the substance. It is figuratively speaking, however, for we should realize that when we remove force C, then the line A-B would disappear also, being but an extension of C.

We can see examples hereof with any magnet. When we hold a piece of steel in front of a magnet, the steel will conduct the force of the magnet, and be very real upon the steel. But when we remove the magnet, the steel will no longer have its lines of magnetic motion anymore. And likewise with electrical currents. When we switch off our lights, the motions upon the substance of the wire disappears.

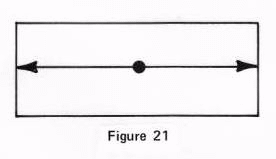
How therefore shall we take a frame and take an outside force, and impose a lining upon the motion of the substance of the frame with this force, and then when we remove our force, to leave us with a self-sustained force of motion that can indeed motivate things without any other help? The answer to this is we must not only induce the force to begin with, but make things so that it remains with two opposing forces within itself over a point of centering, like that drawn in Figure 21.

There are two ways of doing this. We can, for one, make an electric generator, and although, a generator can not make a current fully self-sustained, it maintains a constant opposition by the continual motion of its armature. The second way is to use a certain substance, a metal which has such a structure formation that once its general motion is aligned, it is in fact capable of retaining it under certain circumstances. An example hereof is lodestone.

Equal opposition of motions upon the general motion of a substance can only exist if there is a center between them, for it is over this center that the force switches around, to back-up one half by its other half. And let us be certain that at any time we have a center of force, it extends out in equal proportions in both directions. All of which comes back to the three-point principle of nature, and the law of equivalence.

Instead of beginning with the heart of a magnet, let us begin with the outside appearances. Usually we say that a certain metal, such as steel, has magnetic properties whereby it can be magnetized, and air can not be magnetized, yet we shall see that the air can do what the steel can do, and that only a certain specialty in the way motions are laid forth makes a steel bar magnetic, and most other substances not.

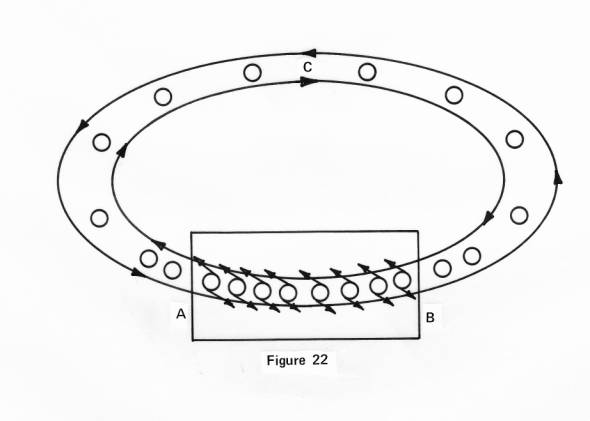
In Figure 22 suppose we take before us a steel bar, and let us represent a few of its atoms or molecules, by the circles which are always turning in circles, but not moving back or forth through the bar, for the bar is solid and everything stays in place, whereby we have motion in place. Then let us suppose that somehow we take a line of force, and use it so we can turn all these atoms and molecules around in such a way as to line up with one another to make but one straight line instead of many lines in all directions.

 

This is simple to realize. And yet we may question why we should have one direction, while by a circle we could have 360 directions. The answer, and secret to this, lies in the multiplication of things, for note how from A to B, the motions can make one long line of motion, and by equalization another long straight line of motion goes directly opposite it on the opposite side of all the circles. If we wanted more directions we could begin by lines directly vertical to the first, but they would have to pass over, around or through the others, would they not?

And suppose we argued that the first circle past point A were orientated so that it would direct its motion inwards, between it and the second circle, which would break up the line. If others do the same or cast it in some other direction, we would have no line of motion to one direction, or two.

But consider now that if this circle were to do this, would not that motion come to move against that of the second circle as it comes up down there? Therefore by their combined motion the first circle would naturally, or forcefully, have no choice but to cast its motion just as we showed. And within a circle it already appears that it is difficult to end up with more than two main general lines of motion.

And yet this is hardly the main reason why we have specific lines, for we must realize that atoms have motion in a circle by their electrons orbiting the nucleus, but quite a number of the atoms combine together to make a whole molecule, which is the first beginning of a structure. And by this very combination of atoms, many of its 360 possible directions have been eliminated, and as a whole, the molecule is limited even more.

It is in fact specialized to points which rarely if ever exceed the number 10. A square has 4 points, a triangle but three, and then there are hexagons, etc. This can be substantiated by those people who perform research in the structure of matter.

Our circles in Figure 22 should therefore be considered systems greater than any atom, and a molecule is the least thereof. A structure which is very simple and very basic, such as hydrogen gas, or air, or water, is much too simple to really be able to concentrate an entire formation of magnetic force upon it. Therefore it is non-magnetic.

In order for a substance to be able to hold a magnetic force, quite a number of molecules are required to form but one section for a line, such as we show by a single circle in Figure 22. Therefore immediately we realize that the lines of force of a magnet are spaced apart considerably, or else we should not be able to fit so many molecules between a coming line and a going line.

In the drawing we further indicate that this line of force is continued on by the substance on around the magnet. It is the power of the motion of the line between points A and B, which continues to align the substance of the air, although the air is not drawn unto the magnet, even as the molecules within the bar itself are not really drawn unto each other. Why should they? They merely line up by an impulse to face in a certain direction, we might say, because this alone, or this by itself, is not yet motivation to pull another magnet or so unto this one.

Right now however I want to point out a most interesting fact about third order magnetic motion. It draws lines in a curve, and by that I do not mean it draws quick circles, but it makes curvatures out of every straight line. It bends a straight line only slightly, making for great circles or curves, which enables the force to be independent in the first place, and in a second place to really motivate magnetic objects. As the motion goes out of the bar at point B, it turns about and comes back in it at point A making for a perfect balance within itself.

One could well imagine that if, for example, the motion went both directions out of the bar from its center, then somewhere they meet at point C. Where would the motion load itself upon there, and unload itself in the middle of the bar? These things are not possible, for as we should realize within this circle of motion there is no supply nor demand, but a continual motion in place that has itself lined up into the design of a circle, and to unload or to load at any one point, such point is non-existent. There would be no balance or equalization if such things existed. The law of equalization not only forbids this, but makes such things only a myth.

Concentrate now, and consider comparing this motion of force with those of radio waves or light. For if I the line traveled on in a straight direction, it would always continue on and never meet any other line. Nor could it re-supply itself (figuratively speaking), for its line would continue forever straight in the other direction "also, or unto such a point where the intensity of the line , has decreased so greatly that we no longer can speak of a line or alignment.

It is the curvature therefore which enables it to be a unit of force in itself, about but one bar in one place, while radio waves travel away in straight lines. They are ; not lines of the third order of nature, but of the second rather. Or if for our convenience, we assume a radio wave to be the line of motion set forth by the circles of the substance, then our bar would never be the magnet we know, since by the straight lines of motion passing through it, it is just a bar passing on a vibration of that line.

And at this point, we begin to realize how the third order of nature is a magnitude, entailing forces of special alignment, that is to say, only such forces as are not quite natural by and in nature itself, because an outside party, other than a mathematical formula alone, is required to start them, and when electrical, to continually maintain them.

What is the basic cause, or the foundation then, which enables a magnetic force to assume a curvature and become the force it implies, the structure of the substance? And if and/or when the structure is such that it can both make and conduct such curvatures, but it can not really hold on to them by itself, such as regular steel, it requires a constant motion of a third order magnitude upon it. It can not just be any motion, therefore, but motion very much relative to its own design.

These .things are detailed under generating and the principles of magnetic forces in my first volume, and too complex for our general description here.

Returning to Figure 22, we note that the second line of motion on the opposite side of the circles is moving in the opposite direction to the first, therefore there is mo­tion in both directions in the bar and outside of the bar. How shall we thus speak of a positive and negative side, or north or south pole, since we must interpret such things by direction only? The answer to this is, there are no positive nor negative sides, and as of yet the bar is not a magnet, but we have completed our first step to gaining insight therein.

Both lines in Figure 22 are equal in power and equal in all other aspects, one balancing the other, whereby as much motion and direction of flow is going into the bar as there is going out of the bar. The net result is zero polarity.

Let us then look at our line of curvature in Figure 23 as it extends through the bar from A over D, to B, and find that there is no equalization anywhere. The distance of potential force or motion of the substance of the bar is greater from C to D than it is from D to E, and at the ends likewise, and no force could long exist with such an unbalanced proposition. 

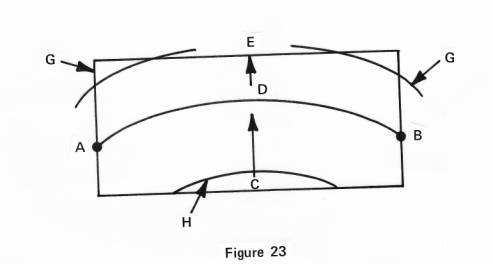
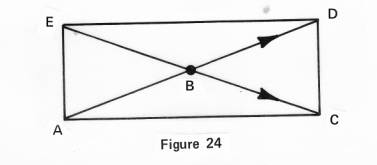
Also it is not likely that a second line of curvature should span but a fractional part of the length of the bar as demonstrated by line H or line G, for no matter how we look at it, the illogic of balance is certain. But as we know already, forces will seek their own balance. Therefore when we again take our line of curvature in Figure 24 to span from points A-B-C, the line beginning at A will end up at D, and the line ending at C will begin at E, for several reasons.

First of all, because it seeks balance, and as it seeks this balance it twists itself as we twist a wash-towel to squeeze out the water, and secondly, the very curvature, or formation of its motion, follows that circle we spoke about, and as it comes around and back in at the other end, it completes a figure-eight, demonstrated in Figure 25. 

  

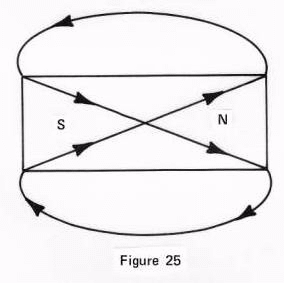
If thus we compare these two pictures, Figure 24 and Figure 25, and consider when a thing is twisted, the line of curvature which was from A-B-C, has become one and the same line, or is one and the same line from points E to B and C. Follow this in the figure-eight, in Figure 25 and note how equal this force is. Not only has it perfect balance all throughout, both force-wise and by its motion in both directions, but it yet has but one direction of motion within the bar itself.

And the bar as the bar alone is but one-half of the real contingency of the force in its complete entity. And with this one direction we now are able to obtain motivation unto other objects in relation to this one or vice versa, and we have polarity of course. We do not have straight lines going from end to end, therefore we can not find the force to concentrate on a needle-point center, nor can we find straight lines in a magnet such as this except as drawn, from the bottom of one end to the top of the other side.

You can take any magnet and you will find that everything said here is very true, and confirmed by anything and everything in nature that is magnetic (as magnetic, not electric). Some of us may say, "Well, but that is a big order to state, that nothing in nature would prove to be different in that respect," but big or not, it is true, and I can't help it any more than you can.

If we take another magnet that is considerably smaller than this one, and we face its north end to this south end, we shall find that it tends to pull away from the center of the bar, or force, which is logical because the motion is a figure-eight, and in a curvature it draws away from the center. I have assumed that the flow of motion is from south to north in the bar, and the other way around outside the bar.

If this is really so, I do not know, but it must be one way or the other. Of course any side could be called north or south, but our north upon the earth is by Greenland and if this shall be standard, and we can determine the actual flow of the earth, then we make the flow according to that standard.

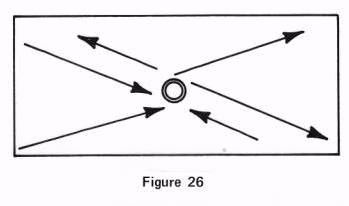
There is more to this force in respect to the point of center or neutral as we usually call it, demonstrated in Figure 26. Each line goes through a changeover as it passes the center. Nevertheless the lines are maintained intact, and while I demonstrate it as if they require going partially around a circle, it does in fact accomplish this by what we can best visualize as a twist in the line, or a re-positioning.

Therefore it is well to realize that the center indeed is neutral, for it is a switching point. And on one of the lines I drew the return line of motion, to get you all confused again. For with an equal return line, also in a figure-eight, we are left with no polarity again, and no magnetic force likewise. One must realize then, that the one little circle I drew is merely a representation to begin to convey things, but that a center of a force should be more than just a little circle of motion, for it comes down to an area at the final result.

The center of our earth for example is not a needle-point so far as gravity or its magnetic force is concerned, but a spherical area. Therefore I am not wrong in describing it as a ball or a circle, but what this concedes is quite a story. To demonstrate graphically how the force principle proceeds through it is shown in Figure 27.

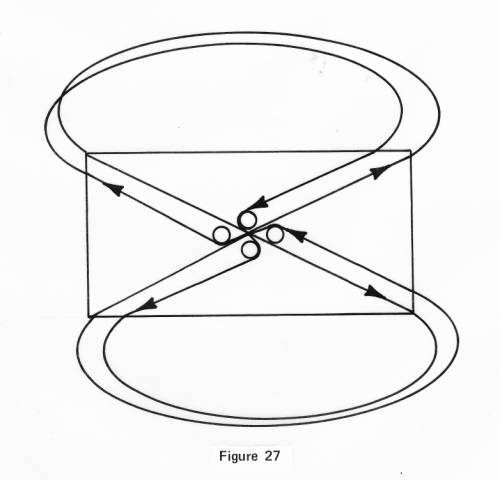
Note how the center is demon­strated by four circles, and how the first and original line of the figure-eight does indeed remain intact throughout the area of center, while its return line does not, but must make such a turn in switchover that it is considered broken as far as it concerns leading motion, which part we shall explain under electrical motions.

Moreover, the return line twists, and while the picture shows the return line crossing the main line at the center of the curve outside of the magnet, it does never physically cross it, but turns about it one-half of a turn for each half of the figure-eight. It begins this as it leaves the center and in that gradual fashion completes it when it returns to the same center of the opposite side.

One should again realize that this is but a most general explanation, like the A,B,C of the alphabet. And to put it most simply, one motion always leads while the others lags or lacks. One is fully based; the other is inter­mediately based, and loses the lead by it.

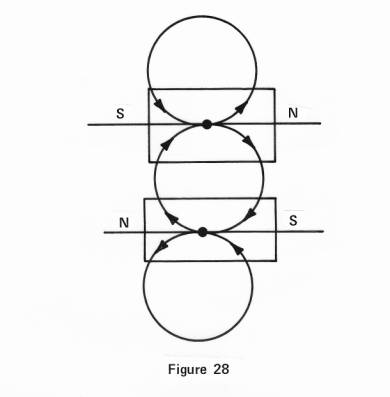
Now are both lines considered equal in all things (except as mentioned) in respect and in relation to itself, but in relation to another body, or force of identical credentials one line, one main motion determines and rules the motions of the whole body or force. One example, we show in Figure 28 with two magnets parallel, and north and south near each other at either end.

We note by the arrows on their figure-eights that they flow into each other and combine as if they were twins, or one being between them, making their two circles as one circle, one binding the other by their center or over their center points. Not that any force pulls from a center. It is just that all pull always comes on over a center therefore it may appear unto us as if all pull is always concentrated at a center. As we say, the earth acts as if all its mass is concentrated at its center, because gravity, and magnetic force appear to do that. Things are not always, therefore, what they appear to be at first sight. It is the understanding of the nature of a thing that reveals what is real and apparent.

 

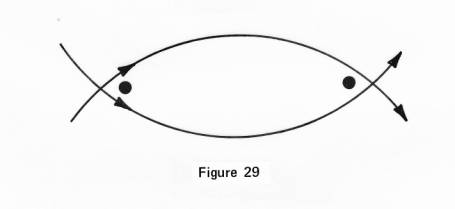
When we try to explain motivation, we use these center points in their relation with the lines of motion in the manner in which they pass over it, for by that fashion we can vividly see and realize how one may be drawn to the other, which I show in Figure 29, crossing over, forcing the points to move, like blood is pumped in an artificial heart machine, or like bringing a object unto you by throwing a rope over it and the motion of the rope in its curvature brings the object unto you.

But things can not always be shown to move by such embracing, for repulsion is the opposite, and there we must realize the real mover, namely the motion of the line it­self to separate two points from each other as in Figure 30.

 

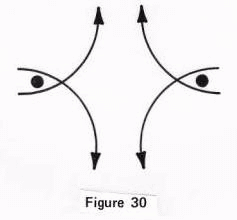
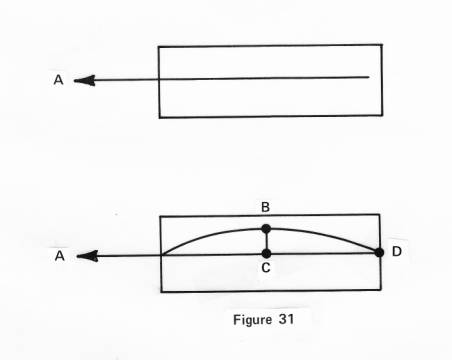
One more thing I wish to show, and that is drawn in Figure 31. Suppose we take a magnet, and let point A be this magnet. Then we place a regular piece of steel nearby. And let us suppose for the moment that the line of motion is straight, and passed into the steel that way. If thus we pulled on the line with point A, our magnet, the line would come right out of the steel, and the steel remain where it is, while if the line were a curvature and we tried to pull it straight out, the steel may be taken with the motion because the volume residing in the area between the lines B-C-D might act as a resistance. Point D must pass over point C, but in order to do this it must physically pass sideways over this volume. 

Another example is if a ball be on a table and it can not move side­ways, and we take ourselves a straight stick, we might turn the ball but not bring it to us. But if the stick were a curved one and we moved in a straight line we could indeed bring the ball unto us. 

This is of course a hypothetical example, for a magnetic force to so bring a regular piece of steel unto a magnet. Yet in so many words we are not far off, because curvature does indeed lay a good hold on the structures of substance, but not on all structures, for we could not do the same thing with copper or silver.

The structure of the substance therefore determines whether a curvature shall be allowed to grasp it firmly or not, and when so, moves it by the motion of the force, together with its center points and curvature in relation thereto. 

This is one way of saying every part and every factor is required in unison, to perform any one or all of its functions. Herewith I shall end our discussion of the magnet. For anyone who wishes to see the principles of its more fundamental motion, they are written in my first volume.