

 “Inertia”
“Inertia”
CHAPTER
40 ![]() INDEX
TO OTHER PAGES
INDEX
TO OTHER PAGES
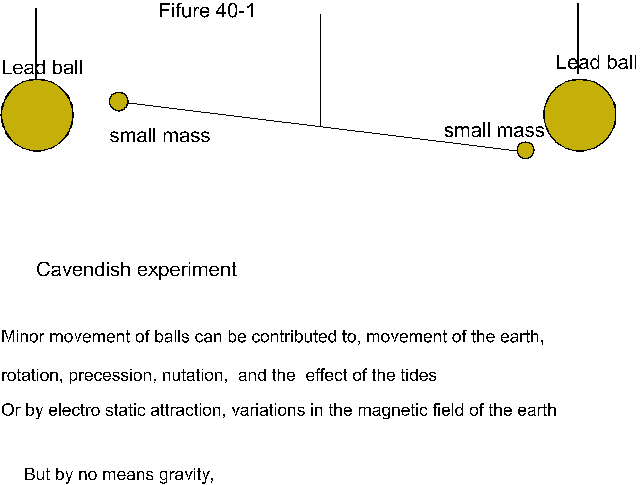
The more we know about the particulars of a phenomenon the better our understanding of the whole will be. Inevitably therefore we trace our past and bring forth current ideals that do not fit the picture, one such is what is known as the Cavendish experiment figure 40-1.
The attraction between the balls was used to measure the mass of the earth, because – erroneously – it was conceived the force of that attraction to be gravity.
One obvious flaw in that experiment is for the so-called gravity waves to pass into the wrong direction, the direction of gravity is directly downward to the center of mass and never at right angle thereto.
When by figure 40-2, we view the atomic gyro listing an inertial resistance of 32.14ft/sec, it not only means that this gyro is pulled by a force to that extend, but as I cleverly noted – it responds equally with inertial “resistance”.
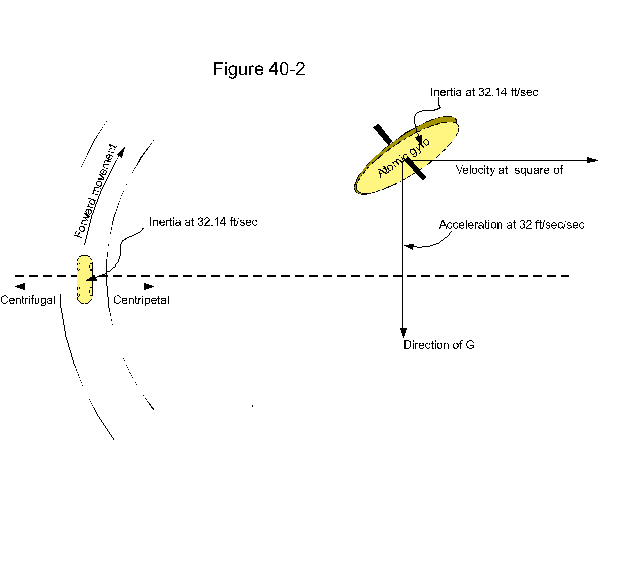
We may have the idea as if the force that pulls the gyro down is one of that particular measure - viewing the gyro as an object to bring down to earth.
But this is not altogether
so, it is equally driving itself into a downward measure effecting the value of 32.14 ft/sec.
If we set the vehicle in motion upon the road at right angle to the direction of gravity, we cannot in that movement speak of a force of gravity. The forward movement is by the power of the engine, while the traction and resistance of the wheels upon the road to force it into a turn is not in any way from a force of gravity.
Nor shall therefore the centrifugal impact, which the car and the driver experience be of gravity, or in any wise a cause thereof. And yet in order to calculate the forces involved in this scenario we utilize the figure of the acceleration of gravity. And why may this be so?
The answer is in what I stated as “inertial resistance”, the gyro’s of which the vehicle is made are the same as gyro “A”. If therefore we elevated it upwards, like unto a rocket we are combating the force of gravity, and we must exceed gravity in all of the force of 32.14ft/sec to begin to lift the vehicle.
At any right angle movement we need only overcome the inertial resistance, the rigidity of all matter to remain in place, or when in motion to remain so in a straight line.
The calculation for this traces itself again to the quantity in the “acceleration of gravity” since the inertia is as much a measure of gravity as it is of its own, a twofold factor.
Note how when computing mass we divide by 32.14, and not ft/sec/sec. When however we compute velocity into the direction of g and to any direction then it becomes ft/sec squared. But here again this is only because force in velocity squares itself upon a twofold factor of inertia, the one of angular and of linear inertia.
The reason for lighter objects to fall at the same rate with heavy objects is in the fact that the factor of inertia is the same for both.
And while it has been said that inertia is synonymous with mass, this cannot be correct, since mass has a fixed measure, while inertia can go to any measure in the velocity placed upon it. The laws of motion are quite clear on this point, with the mathematics to evidence the same. The astronauts out in space do not grow any larger while the inertia of their bodies multiplies.
Consider this; if you had a vehicle of 1000 lb sitting on the ground, it so we presumed had a g/force on it equal to 1000 lb. If then we are to lift that 1000 lb vehicle upwards, we would need no more than any degree of force in excess of 1000 lb. If therefore we applied a force of 1001 lb, it should move should it not?
The correct answer is a yes as well as a no, if it were located directly at the tip of earth's axis, it would, but anywhere else on earth, it would not move since the full and true force of gravity upon that 1000 lb scale weight is compounded with the additional amount of g/force implemented upon it by the centrifugal duress upon it, that exists everywhere on earth, excepting the tips of it axis.
 Evidence by comparison
Evidence by comparison
How are we to say; “Objects attract unto each other proportional to their masses, and inversely to their distance? This cannot be. The sun for example has a diameter 108 times as large as that of the earth, and though the density of the sun may be estimated at 26% to that of the earth, its mass is many times that of the mass of the earth.
Yet its gravitational force in the velocity whereby the angular exceeds into the linear is only 5.26 times as great (136,400: 25,937 = 5.26). And the mass of the moon reported to be 2% to that of the earth has a gravitational force 16.6% to that of the earth.
Certainly therefore, the attraction between the earth and its moon is not according to their masses. All this is assumed
based on man's figures.
Thus we require to know the mass of the moon in weight times the square of its circular velocity, divided by the radius. This will give us the inertial impact into the centrifugal direction, which is directly equal to the gravitational force of the earth upon it.
If then we divide that figure by the weight of the moon (weight as in earth-weight) we will also know what the value of the earth’s acceleration of gravity is at 238,856 miles from the earth. Or if we know the rate of acceleration at that radius, and the computation does not equal, then our measure of its mass or of its velocity must be in error.
I may be quoted to have said - that the mass of the earth has no entry in the computation by which objects are attracted to it, since objects attracted to it are according to the gravitational constant of the earth which happens to be with an entry +/- 32-ft/sec. And exits at +/-25,937-ft/sec (figures at sea level). Or we could say +/-32-ft/sec for the angular and +/-25,937-ft/sec for the linear.
We seem to be certain that mass does not change wherever it be, accordingly, the rate of acceleration can not be the same for a person of 165-lb on earth, compared to 30-lb on the moon. 165-lb means a mass of 5.13, the same person on the moon at 30-lb
divided by 5.13 means there is an acceleration of the moon’s gravity at 5.85-ft/sec.
Since therefore 2 + 2 equals 4, a person of mass 5.13 is not attracted according to its mass - since he is attracted more strongly to the earth, and with yet a greater force to the sun, and with no force at all to a comet where there is no gravitational force.
We lean upon the crux saying; “O but the body, or the mass is so much larger,” as in relative to both masses, and the mass of moon being smaller than the earth, the 5.13 mass would of course have a lesser attraction.
Still,
I say “crux", for is not the moon in its mass reported to be 2% to that of the earth? 2% of 165 then being 3.3lb, how did that person come to be attracted at 30-lb?
Obviously there is something wrong with Newton’s law of gravity
in its vocabulary as in its computation. But I suspect Sir Isaac Newton himself never realized that with his good laws of motion he contradicted his own gravitational theory.
Example. 165-lb x 26400-ft/sec2: 22,176,000-ft/r = 5,186-lb/cg (2,352-kg)
Let us reiterate where we said that the person of 165-lb. had a gravitational pull of 183.24-lb. We know that the force of inertia by velocity - as much as it acts to produce gravity - will also by a force of 5,186-lb overcome the same.
This quantity by a velocity of 26,400-ft/sec and at a radius of 22,176,000-ft, how much will this be at a velocity of 1521-ft/sec with a radius of 20,929,920-ft (on the surface of earth’s equator)?
The force of 18.24-lb divided by g at 32.14-ft/sec = 0.57-lb. which means; this person at his circular velocity has already lost 0.57-lb of his true weight exceeded into the inertia of his velocity.
The true and correct gravitational weight of this person therefore is 165.57-lb, with the correct force into the centrifugal remaining at 18.24-lb.
Enumerating the statistics:
G/force, or centripetal force is 183,24-lb., gravitational weight is 165.57-lb.
spring weight is 165-lb., centrifugal inertia is 18.24-lb.
Now let us place this person in a jet-plane just above sea-level to set his throttle at 1037-mi/hr, which is twice as fast as before Thus 165 X 3026-ft/sec squared, divided by 20,929,920-r comes to 72.19-lb. divided by g at 32.14-ft/sec = 2.25-lb.
He is thus traveling twice as fast yet lost five times as much of his weight. Or we can say, at twice his speed he lost only 2.25-lb of his weight.
Accordingly the “spring”
weight, which previously was 165-lb, will now be 163.32-lb, for we can either take 165.57 minus 2.25, or 2.25 minus 0.57 to 1.68, and deduct it from 165.
The statistics here are:
G/force, or centripetal force is 235.51-lb., gravitational weight is 163.3- lb.
spring weight is 163.32-lb., centrifugal inertia is 72.19-lb.
And it is verified since the additional 1521-ft/sec in his velocity took away only 1.68-lb. of his spring weight, yet it took 2.25-lb. of his gravitational weight.
If then we traveled some 339 mi/hr more than we are, or the earth made one revolution in little more than 18 hours our
gravitational and spring weight would be equal since 165 x 2019-ft/sec2 : 20929920-r = 32.14 : 32.14 =1. For in that case our velocity in force comes equal to the force of the gravitational acceleration.
The statistics for our astronaut then are:
G force, centripetal is 5,186-lb, gravitational weight 0-lb, spring weight 0-lb, centrifugal inertia 5,186-lb.
Suppose the earth rotated at twice its speed to complete each revolution in 12 hours. This would bring the velocity of a person at the equator to twice 1521 or 3042 ft/sec, which in turn would bring the centrifugal impact to 72.95 lb on a person of 165 lb spring weight.
Accordingly, 72.95 lb divided by 32.14 comes to 2.269 lb as the amount of gravitational hold, which is exceeded, into the inertia of his velocity. The spring weight then being 165, less 2.269 comes to a new spring weight of 162.731-lb, or
gravitational 165.57 less 2.269 is 163.3-lb.
Let us now take a traveler in a jumbo jet at 30.000 ft heading eastwards over the equator at 600 mph. The 600 mph adds 880 ft/sec to the 1521 ft/sec or 2401 ft/sec as his true velocity relevant to the earth’s axis of rotation.
In a Westerly direction the 880 must be subtracted from the 1521 to the sum of 641 ft/sec, while the 30,000 ft added to 20,929,920 comes to a radius of 20,959,920 ft. Accordingly;
165 x 24012 = 951,192,165 : 20,959,920 = 45.38 lb of centrifugal force.
165 x 6412 = 67,795,365: 20,959,920 = 3.23 lb of centrifugal force.
The gravitational force on a person thus varies as he travels at some distance above the earth, and into what direction that movement may be, going eastwards the gravitational pull on a person of 165 lb spring weight would be 210.38 lb. And coming back westwards it is 168.23, as less then if he were standing still.
In the easterly direction a total of 1.41 lb is exceeded into the inertia of his velocity, in the westerly direction only one tenth of a pound (0.1 lb) is exceeded into the inertia of his velocity.
In order for one to feel weightless the centrifugal force upon him must come equal to the gravitational pull. Since therefore the inertial gravitational weight of a person will exceed into the inertia of velocity, the squaring of the force, a person of 200 lb must come to a centrifugal impact upon him of 6428 lb, (his weight verses the acceleration of gravity.
This at sea level, the radius thereof would mean a velocity of some 19,469 miles per hour.
The reason the astronauts get by with 18,000 mph in becoming weightless is their increase in radius and decrease in the acceleration of gravity.
And so it seems that the faster the earth turns about its axis the less we would come to weight upon it. If the earth made eighteen revolutions in the same 24-hour period as it now completes one revolution, we would all float out into space together with the waters of the ocean and everything else, or would we?
No, not so likely
since the increase in that movement would also change the rate in the acceleration of gravity, all things being relative.
If I am passing on all this info too fast for others to follow, I suggest to go over it several times, and or study the same. I am nonetheless attempting to be as simple and as elementary as I can be.
FACTORS OF INERTIA.
The force of g at 32.174 (sea level) is what is properly called the factor of inertia, or, the inertial factor of mother earth. It is by that factor that in free fall we accelerate 32.174 ft/sec/sec. It is the draw of the magnetic force of the earth in conjunction with the inertia of all substance at so called sea level.
This inertial factor is not the same for all planets and suns, it is less upon the moon and greater for our sun. It of course exists only on objects that exhibit a magnetic force, since without it there is no gravity. As therefore these factors vary, let us entertain a sum of a difference comparable to something we are familiar with on earth.
Let us assume that our sun at its surface had a inertial factor of 360 lb, and let us assume a person of spring weight at 165 lb. on whom upon the equator of the earth there is an additional 18.24 lb of g force, the total g force on the person being 183.24 lb. How much therefore will that person weigh upon the sun, and what will be the full g force upon him?
We take the 360 and divide it by 32.174 which = 11.19. meaning his factor of inertia at 165 spring weight fits 11.19 times into that inertial factor of the sun, giving him a weight of 1,846.35 lb. Then we must add the centrifugal impact for the additional g force upon him, and the sun being 108 times as large as the earth, his velocity around the vector will be proportionally greater.
Assuming the sun to turn similar to the earth, to have a velocity of once around in 24 hours, we find the distance from the sun's surface to its axis by multiplying our 4000 miles times 108. (not that this is necessarily accurate, but we shall do so for our example). This comes to a radius factor of 432,000. miles, or 2.280.960.000 in ft.
His velocity then in a circle as large as twice 432.000 in diameter, times 3.14 for its circumference comes to 2.712.960 miles per 24 hours, or 113.040 miles per hour, which is 1.884. per minute, and 31.4 miles per second, which converted to ft per second is 16.328.
If therefore we take his spring weight by the factor of inertia of 1846.35 lb times his velocity (16.328) squared, it comes to 492.243.527.318.4. And this divided by the radius comes to 215.8 lb of g force to add to his g force by the factor alone to a total of 2062.5 lb of g force.
So we see that upon the sun with an inertial factor of 360, the additional g force alone on him is more than his spring weight upon the earth, and his scale must be rated for some two thousand lb, in order that it may be read.
I utilized this example so we may not get hung up on the idea as if gravity is the same everywhere, for man is apt to judge everything by what is under his feet, rather than by factual reference.
If then we conclude that by the example the acceleration of gravity should likewise be 360 ft/sec/sec, rather than the 32.174 as it is under our feet upon mother earth, you have a good point, and may very well be so.
Myself I am making no such claim since I would have to dig a little deeper to be absolutely certain before setting any standard in that respect. We could experiment upon the moon with its smaller inertial factor to see if there the rate of acceleration is like unto its factor, if so you will have something concrete for a standard.
The g forces that are upon those large loops of fire that we observe upon the sun are and must be rated according to the factor of inertia that is in conjunction with its overall magnetic potential, that in turn is subsequent to its movement in rotation as well as galactic movement, and the internal movements.
One thing seems certain to me that the sun projects multiple magnetic potentials even though its greater overall span within the solar system appears to be of a single nature. Altogether this makes the sun as yet an interesting project to decipher.
One of the reasons that the scientists claim the sun to mainly subsist of Hydrogen, is because they are still digging for oil to power their toys. These have yet to figure out how to obtain a source of power like unto the sun that is self sufficient and regenerative, never in need of supply and demand, but forever free and clean.
As long therefore as they dig for oil - they will not come to comprehend the nature of the power of the sun. And I am not one to reveal it, nor will they in themselves come to figure it out. These live much too much in a world of fantasy that I should in any way be inclined to them.
As long as man cannot realize his lie in what electricity is, how is he to know what is in the way of fundamentals, or that he should take himself upon my word? I make no secret of it that I have taken my sincere dislike of them.
![]()