This article was send to the Academy of the Advancement of Science. They were very angry with me for daring to send this. See pages 44, 54, 55, 58, 60, and 70 for more detail, or simpler detail. Later on published by JAP
BY A LAW OF MOTION
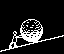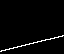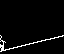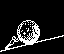INTO THE CAUSE OF GRAVITY
CHAPTER
28
INDEX
TO OTHER PAGES
This
is an in-depth review into the fundamentals of the laws of motion, showing the
cause to gravitational force to come about in the same laws by which it is
governed.
It is mathematically evident that the gravitational pull upon an object is not the same at all points upon the earth, varying by some ten percent from equator to pole, while the oblation of the earth varies by 0.5%. We then may be intrigued to behold how this gravitational force finds its birth by way of “movement into movement upon a twofold inertia".
And
while it may seem acceptable to us that objects are attracted unto one another
proportional to their masses, the evidence in both law and experiment are stacked against it.
Hence, the property of mass that gives rise to its force of
attraction is found to be “its own movement".
The illustration figure 28-1 in its singularity then shows it all, but like our laws it requires definition to bring it home.
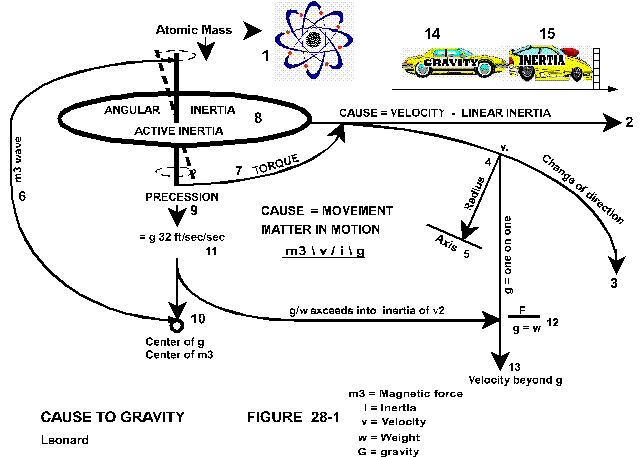(Click the link for larger illustration)
INERTIA
Inertia, as a single phenomena is effectually twofold in its angular and linear
forthcoming just as movement is by either a circular or straight path. The fundamentals of either being alike, we should therefore
address each one individually to establish their basis in the scheme of things.
Angular
inertia shall refer to the atomic momentum (Figure 28-1-1) the
movement of-atoms in their system providing the inertia
for the atomic mass, which hereinafter will be referred to as either the first or angular inertia.
Linear inertia, or second inertia (Figure
28-1, 2, & 3), is the inertia by velocity (or speed) to include the inertia
by a change of direction, and/or of a change in the rate of velocity. For
since that inertia is of the whole of the mass, or of the object in motion,
it as such is distinct from the first. For
gravity likewise acts differently from the first to the second.
Upon the first inertia there is a fixed momentum of gravitational force in the acceleration at +/-32 ft/sec/sec. (Figure 28-1, 11). In the second, the velocity to which gravity will apply, is higher, and without a specific rate of, coming to 25,937 ft/sec (at sea level) when it will have exceeded its first component, the angular inertia exceeding into the force of the linear.
It
is here where gravitational force loses out to velocity. These
figures then are in the calculations of the Earth’s gravitational force and
not necessarily of any other planet or star.
In the calculations of the angular inertia or the force of gravity thereon,
radius is not utilized since gravity applies itself on this fundamental movement
of nature at (so called) random, which will clarify itself as we go on.
Nor
in this case can the velocity of the circular movement (linear component) be
utilized, since gravity has already an acceleration by distance in time ascribed
to it. Any other rate of velocity
can not therefore be used.
In the calculation to linear inertia (circular velocity) which takes in radius (Figures 28-1, 4 & 5) and the velocity to the square thereof, gravitational pull accompanies the same in equal measure to the point where the force of the first exceeds into the second.
This
is given as (F/g = w, force divided by the acceleration of gravity to equal the
weight of the mass, (Figure 28-1, 12 & 13).
As thus gravity is the cause in the first with inertia the reaction, in
the second velocity is the cause with gravity in the reaction.
BY LAW OF
FORCE
In the calculation for the gravitational weight of a person we need more than just the figure of 32-ft/sec, we need to know mass. And if mass is known by weight, we need no longer compute the same - the weight being known.
As per example, weight at 165-lb. x 32.14-ft/sec = 5303.1 divided by 32.14-ft/sec = 165-lb. of gravitational force. But in order to complete the calculation of the full and true measure of gravitational force on any person, we need to add the centrifugal impact. Accordingly, a person of weight 165-lb. at earth’s equator is, weight (w) times velocity2 (v2) divided by radius (r) (w x v2: r)
Example # 1. 165-lb x 1521-ft/sec2 : 20,929,920-ft/r = 18.24-lb (8.27kg)
The outcome is one of centrifugal impact counteracted by an equal (one on one)
amount of gravitational force. (Figure 28-1, 4/5 and 4/13). This
added to his weight (as likewise a measure of g), proves the person to have an actual gravitational force acting on him of 183.24-lb/g, (83.12kg). This
is absolutely correct unless one can certify that Newton’s first law of motion
is incorrect.
Thus we find gravity by “two” computations, the first on the angular inertia by +/-32 ft/sec, (9.75 m/sec) located at random. And the second, by velocity in linear inertia at its speed in ft/sec2 bearing its radius to earth’s axis.
Definition to “location at random” is; that the direction to which the flow of gravity is directed, is a separate cause from its application to the “first inertia".
For
as with the linear inertia having its radius along the entire axis of the earth,
the mass bearing the inertia is nonetheless directed to earth’s center. Equally
so, the first inertia, being nothing more than the angular moment of the mass in
all of its atomic gyro’s, bears no center in itself, yet is drawn to a center
of.
What
therefore would the gravitational pull be on an astronaut 200 miles above the
earth? Assuming velocity at 18,000-mi/hr, which is 26,400-ft/sec,
and the radius of 4,200 miles in 22,176.00-ft. (cg meaning, c for centrifugal, g
for gravity).
Example
# 2. 165-lb x 26400-ft/sec2: 22,176,000-ft/r = 5,186-lb/cg (2,352-kg)
If it were not for the force of gravity to counteract the great impact of centrifugal on him, the man would be crushed to death under the weight of more than 2 tons. Our astronaut however feels no weight, and how may we know that? Simply by dividing the g force into the rate of acceleration of g, which at 200 miles up is 31.34-ft/sec (9.57-m/sec).
The resultant being 165-lb. (his weight) means, that all of his weight (first, fundamental inertia) has been exceeded by or into the inertia of his velocity (F/g=w).
If we ask, why does he have to travel at 28,967.4-km/hr. and +/- 6759-km/r to have a stable orbit in order to feel himself weightless? There is a computation to show the same, but the herein following computation is another that goes deeper into the nature of gravity.
Assuming
to slow him down to 26,000 ft/sec, Example
# 3.
The resultant of 160.5-lb. means that he still has 4.5-lb. of his angular inertial weight on him to come to a state of weightlessness, or he will be pulled down by that remainder of his weight. Simply said; one cannot be weightless lest all of his weight is exceeded into the (his) inertia of velocity.
If
next we maintain velocity at 18,000-mi/hr, but decrease radius to 22 million-ft;
Example
# 4. 165-lb x 26,400-ft/sec2 : 22,000,000-ft = 5,227.2-lb/cg : 31.34 = 168-lb,
The +3-lb. over his weight here means, that his weight has been exceeded too far by 3-lb. gravitational force not being able to hold him back against the inertial force of his velocity, resulting into him being driven into a radius wherein his gravitational weight will balance out.
Gravity
therefore, wherever a person may be on the surface of the earth or up in space, will draw upon all mass according to its first inertia by a velocity limited to +/-32-ft/sec. (better
said: - by the g/factor of +-32.)
This shows that there is no radius, nor speed of any mass in or out of orbit to enter into a calculation of weight as a measure of gravitational force. And also to reveal that all linear inertia is incidental, a separate cause, a force into the centrifugal, not of gravity.
But
that the same is counteracted by the gravitational force in a measure ounce for
ounce (one on one) to the limit of g - where the first angular inertia is overcome (exceeded into) the
linear inertia.
I am repeating this for you to dwell upon. :: where the first angular inertia is overcome (exceeded into) the linear inertia.
Consequently, if inertia were a single component, our weight upon the earth would vary from equator to pole, and we would not be able to fly an SR-71, nor venture out in to space short of being crushed by our own weight.
And angular inertia, as no more and no less than the angular momentum of each single atom and the quantity of them in any single mass (upon which gravitational force bears down, or attaches itself), is as such distinct from the linear inertia by velocity
RELEVANCE OF
GRAVITY AND INERTIA
When we say: “the acceleration of gravity is 32-ft/sec/sec", it has its reference to the potential of gravity to impose upon and accelerate any mass subject to it by that specific rate. And also meaning that at each successive second the velocity of the mass will increase by said rate to a terminal velocity that has yet to be established.
This sum (of the acceleration) shows gravity for its force as well. For it means that gravity is such to forge a specific measure which by consequence becomes likewise a measure of the inertia of the mass.
This
may be enhanced when we realize how the force upon a 10-lb. ball in free-fall is
by 10-lb., and that of a 2-lb ball by 2-lb, both falling at the same rate.
And so we must come to the question that while gravity displays a force of a
certain measure - if that measure for its quality and quantity rests in the
inertia of the mass, specifically the fundamental angular inertia, or that it is
an exclusive agent of gravity? If
of inertia, then the measure of 32 ft/sec would apply to all inertia, which is
not the case with the linear inertia.
And if exclusively of gravity, how does it apply to inertia in a case where for example (example 5) a vehicle makes a turn on the road, the cause not being of gravity - yet the computation thereof is used?
A
vehicle, weight 3000 lb, at 22ft/sec, in 100 ft radius (wxv2: gr) or (wxv2: r)
Example # 5. F= 3000-lb: 32-ft/sec/g = 93.75-slugs x 22-ft/sec2 : 100-ft/r = 453.75 lb
Or
again by example, a vehicle at 3000 lb to go from 0 to 88ft/sec in 10 seconds
Example # 6. F=
88-ft/sec : 10-sec = 8.8-ft/sec//3000 : 32-ft/sec/g =
Or a vehicle, 3000 lb from 0 to 321.4ft/sec (219 mi/hr - 352km/hr) in 10 seconds
Example
# 7. F= 321.4-ft/sec : 10-sec = 32.14-ft/sec, then 3000 : 32.14-ft/sec/g =
In none of the above is gravity the cause, yet the inertia acts as though it
applies or contains the constant of force which at all times is called “the
acceleration of gravity” rather than of inertia.
The reason for this is quite simple, by a scenario (at which we will come back later on) the earth in its force towards gravity applies a torque upon the angular inertia of all mass to impress a movement, or a potential of the movement which we call “precession."
It is
at this point where the fundamental atomic inertia is considered active to
present a show of force - that is of course according to the cause (g) at a momentum of 32 ft/sec.
Thus as gravity applies itself to the angular inertia at this enduring constant, so the now active inertia behaves in the same manner. And may be likened to a vehicle called gravity (Figure 28-1, 14). Which, traveling at a speed of 32 ft/sec came upon another vehicle called inertia (Figure 28-1, 15). Which does not have a drive train of its own to push that vehicle along with itself at the same rate of speed.
And to visualize a constant force to one direction while the vehicle does not move, we need but liken car 14, or both cars 14 and 15, at a standstill against a wall with the engine of the driving vehicle still running maintaining a momentum equal to 32 ft/sec.
Take
away the wall and the vehicle will accelerate by (presumably) 32 ft/sec/sec.,
(not real) Or
take away the ground under ourselves and we will fall by an acceleration of 32
ft/sec/sec., (real)
It should thus be evident that gravity is able to apply itself to angular inertia, to that movement of matter, which is said to have a rpm, and that it is not able to attach or apply itself to linear inertia.
And to enhance this, consider the mass in its atomic substance to have this
32-ft/sec impression of force in a single downward direction. Next,
we cause this mass to move into a direction at right angle to the first at some
considerable rate of velocity.
What then shall the inertia be that is added hereby? It is not as we would say “an rpm", but of a linear nature that tends to keep it at speed and into its straight-line trajectory. (Figure 28-1, 1-2).
While this mass thus was accelerating there was a resistance; namely the angular inertia wishing to stay put. And coming to a constant velocity, the added linear inertia seemed to have vanished, leaving only the angular inertia active at its 32-ft/sec impression of force. This impression however is a force to bring a downward movement to the mass (Figure 28-1- 7, 8, 9, & 11) wherefore the mass is forced into a “change of direction” (uniform angular movement, figure 28-1, 3).
The instant this occurs, the potential of the linear inertia becomes active to apply a greater precessional impact upon the wheel (the wheel as fundamental inertia), upon which gravity is able to apply itself.
Consequently
it (indirectly) will increase itself upon the mass by a measure that is ounce for ounce equal to the centrifugal cause. This
is evident in that the gravitational force upon the impact to the centrifugal is
neither registered nor felt by us.
EXCEEDING
GRAVITY
As thus the implementation of gravity on us is limited to be gentle with a mere 32.14 lb at sea level. The same is not quite that gentle on the wheels of nature to forge a precessional momentum on them to the tune of 25,937 ft/sec (790,560 cm/sec) (at sea level).
Were
it not for gravity to equally offset that velocity, we would not be able to
travel at high speed, or be crushed to death by our lady of gravity.
Nor would there be a standard of weight but to vary from equator to pole.
The experimental data we gained from placing satellites into orbit, and the mathematics thus provide us with evidence that gravitational attraction - like inertia - is twofold, and that there are limits to one as to the other.
And to enhance our understanding in this second limit where gravity gives out altogether at the point where the angular inertia succeeds into, or exceeds into the linear inertia by velocity, let us turn to an example of a satellite into an orbital path.
The vehicle will have a fundamental gravitational weight of 3000-lb (1,360.8-kg). And given a velocity of 26,400 ft/sec, which is equal to 18,000 mi/hr or 28,976 km/hr, at a radius of 4,200 miles, which is apr.200 miles (322 km) above the surface of the earth, and let us behold what expires.
Example
# 8. 3000-lb x 26,400-ft/sec2 :
22,176,000-ft/r = 94,286-lb/cg
Then,
94,286-lb/cg : 31.34-ft/sec = 3008-lb, or: by 31.43-ft/sec = 3000-lb
Then,
94,286-lb/cg less 8 lb/v = 94,278-lb/g.
The mathematical formula shows a force of 94,286-lb. of centrifugal impact attempting to drive the satellite into a straight-away trajectory. If then we wish to know if at that given speed and into that radius the satellite will find a stable orbit, we simply divide the force by the acceleration of g at that radius.
If the acceleration of g at said radius be 31.34-ft/sec - the resultant will be 3008-lb, or 8-lb in excess of its weight. This in turn means that either it has exceeded in velocity, or an increase in the radius is required in order to attain to a stable orbit.
If
instead we are in error, and the satellite does maintain a stable orbit at the
given speed and radius, then the acceleration (Factor) of gravity at 31.34 is in error,
and should be 31.43-ft/sec.
Assuming the first is correct, how much of the 94,286-lb/cg is of C, and how much of g? Obviously C claims the full 94,286-lb, since all of it is inertial gain by velocity. But since there is 8-lb. in excess to the weight of the satellite - driving it away from the gravitational center, the net gravitational force on the satellite in this instance is 94,278-lb.
In
a next example (example # 9) let us bring back the satellite to a place at earth’s
equator and find the gravitational force acting upon it. The
velocity will have decreased to 1521-ft/sec, and radius down to 20,929,920-ft,
leaving us with a centrifugal impact of 331.6-lb.
Example
# 9. 3000-lb x 1521-ft/sec2 :
20,929,920-ft/r = 331.6-lb/c + 3000 =
The satellite went from a gravitational force in excess of 94,000 lb down to 3,331.6 lb, and none of its components came back crushed or damaged since the force is placed upon each individual atom, and the net force is the sum of its atoms. If therefore we can number the atoms within that satellite we can determine the net force on each individual atom.
Accordingly it is evident that we cannot add more force to the vehicle and at
the same time expect gravity to hold onto the same. From
here on the force of inertia by velocity will take over in a drive away from the
earth only to become subject to another gravitational force. One
with a higher limit, that of our sun, which according to the information given
is at 136,400-ft/sec to leave our solar system.
COMPARISONS
How then are we to say “objects attract unto each other proportional to their masses, and inverse to their distance? The mass of 94 slugs drawn to the earth by a force of 3000-lb while it is within 4000 miles of its center, comes to have a gravitational attraction 28 times as great when it is 200 miles further from center - where instead an inverse calculation should apply.
Somewhere along the line we omitted to insert movement into our mathematics and into our vocabulary. It should be to say that; objects attract unto each other by forces according to their relative movements and the inertia of their mass.
The sun for example has a diameter 108 times as large as that of the earth, and though the density of the sun may be estimated at 26% to that of the earth, its mass is many times that of the mass of the earth.
Yet its gravitational force in the velocity whereby the angular exceeds into the linear is only 5.26 times as great (136,400: 25,937 = 5.26). And the mass of the moon reported to be 2% to that of the earth has a gravitational force 16.6% to that of the earth.
Certainly
therefore, the attraction between the earth and its moon is not according to their masses. In
fact, the mass of the earth has no entry in the computation whereby the moon is
held in orbit around the earth. The
only time when earth-mass enters a computation is to find the sun’s
gravitational force on mother earth.
Thus we require to know the mass of the moon in weight times the square of its
circular velocity, divided by the radius, (radius from center to center). This
will give us the inertial impact into the centrifugal direction, which is
directly equal to the gravitational force of the earth upon it.
If
then we divide that figure by the weight of the moon (weight as in earth-weight)
we will also know what the value of the earth’s acceleration of gravity is at
238,856 miles from the earth. Or if
we know the rate of acceleration at that radius, and the computation does not
equal, then our measure of its mass or of its velocity must be in error.
I said that the mass of the earth has no entry in the computation by which objects are attracted to it, since objects attracted to it are according to the gravitational constant of the earth which happens to be with an entry +/- 32-ft/sec. And exits at +/-25,937-ft/sec (figures at sea level). Or we could say +/-32-ft/sec for the angular and +/-25,937-ft/sec for the linear.
We seem to be certain that mass does not change wherever it be, accordingly, the person of 165-lb. on earth that will come to weigh only 30-lb on the moon, - will not be at the same rate of acceleration there as he was on earth. 165-lb means a mass of 5.13 that comes to 165 by the multiplication of g. The same person on the moon at 30-lb divided by 5.13 means there is an acceleration of the moon’s gravity at 5.85-ft/sec.
Since therefore in my book 2 + 2 equals 4. A
person of mass 5.13 is not attracted according to its mass - since he is
attracted more strongly to the earth, and with yet a greater force to the sun,
and with no force at all to a comet on which there is no gravitational force.
If the earth were half the size of the moon with its gravitational force remaining the same, the moon would have the same gravitational attraction on it as now. Except of course that the moon would then take our earth to yonder places because the inertial value of the earth would be too small against the greater inertial value of the moon.
We of course lean upon the crux saying; “O but the body, or the mass is so much larger,” as in relative to both masses, and the mass of moon being smaller than the earth, the 5.13 mass would of course have a lesser attraction.
Still,
I say “crux", for is not the moon in its mass reported to be 2% to that
of the earth? 2% of 165 then being 3.3lb, how did that person come to be attracted at
30-lb?
Obviously there is something very wrong with Newton’s law of gravity in its vocabulary as also in its computation. And do not quote me that I purported us to find the value of the earth’s gravitational force on the moon by our law of centrifugal, or centripetal.
For there is something different with our moon compared to any other rock or spaceship floating around us, namely; the moon is a magnet, it has magnetic force, and as such it presents a gravitational force.
And while our calculations may be fine for a nail or a marble floating around a magnet, it becomes a different story when one magnet begins to orbit another magnet in terms of attraction to one another.
There is of course, as I unquestionably know, but one force of attraction which, like everything else may be found or expressed in twofold, namely; the force of magnetic with gravity in its twofold nature.
Find an object without magnetic force and you shall not find gravity thereon. And find me gravity and you will find magnetic force at the center thereof.
For
while neither one is without the other, the male can nonetheless be without the
female, but gravity (the female) cannot be without the man, her birth and
forthcoming is of man, and her return is into him.
(this goes for man as well as nature) These
are the laws of nature that no man can change. And
man’s denial thereof is only his loss
STATISTICS
Let us reiterate example 1, where we said that the person of 165-lb. had a gravitational pull of 183.24-lb., 18.24-lb. of which was due to a cause other than gravity, to leave 165-lb in a cause by gravity. But shall this be fully correct? For since we know that the force of inertia by velocity - as much as it acts to produce gravity - will also by a force of 5,186-lb (example 2), overcome the same?
This quantity by a velocity of 26,400-ft/sec and at a radius of 22,176,000-ft, how much will this be at a velocity of 1521-ft/sec with a radius of 20,929,920-ft (on the surface of earth’s equator)?
The force of 18.24-lb divided by g at 32.14-ft/sec = 0.57-lb. Which means; this person at his circular velocity has already lost 0.57-lb of his true weight exceeded into the inertia of his velocity. The true and correct gravitational weight of this person therefore is 165.57-lb, with the correct force into the centrifugal remaining at 18.24-lb.
Enumerating
the statistics: g force, or centripetal force is 183,24-lb., gravitational weight is
165.57-lb., spring weight is 165-lb., centrifugal inertia is 18.24-lb.
Now let us place this person in a jet-plane just above sea-level to set his throttle at 1037-mi/hr, which is twice as fast as before Thus 165 X 3026-ft/sec2 divided by 20,929,920-r comes to 72.19-lb. divided by g at 32.14-ft/sec = 2.25-lb. He is thus traveling twice as fast yet lost five times as much of his weight.
Or we can say, at twice his speed he lost only 2.25-lb of his weight. Accordingly the “spring” weight, which previously was 165-lb, will now be 163.32-lb, for we can either take 165.57 minus 2.25, or 2.25 minus 0.57 to 1.68, and deduct it from 165.
The statistics here are; g force, or centripetal force is 235.51-lb., gravitational weight is 163.32- lb., spring weight is 163.32-lb., centrifugal inertia is 72.19-lb.
The reason that now his gravitational and spring weight are the same, is because we set our standard of weight free of centrifugal inertia, otherwise weight would vary from equator to pole. And it is verified since the additional 1521-ft/sec in his velocity took away only 1.68-lb. of his spring weight, yet it took 2.25-lb. of his gravitational weight.
If
then we traveled some 339 mi/hr more than we are, or the earth made one
revolution in a little more than 18 hours our gravitational and spring weight
would be equal since 165 x 2019-ft/sec2 : 20929920-r = 32.14 : 32.14
=1. For in that case our velocity
in force comes equal to the force of the gravitational acceleration.
The
statistics for our astronaut (example 2) then are;
REASONING
I know that what I call a constant of gravity, and what currently is held as a constant of gravity are not the same. But then I cannot accept that when two balls at right angle to the direction of gravitational attraction are attracted to one another by some electro-static or other phenomena, to interpret the same for gravity, since that phenomena has clearly nothing whatsoever to do with gravity.
Nor can I be in error here unless we can prove how for a 3000-lb vehicle sitting on a roadbed will require all of 3000-lb of force to cause it to move. If then my drift is not realized how is one reading?
The constant of which I am speaking is relevant only to this earth, and to find a universal constant is simpler said than done, since question number one is; if there is such a constant?
When we state “that every particle of mass within the universe attracts every other part”, we are right but also mistaken by the evidence that our satellite provided us with in the example # 8, wherein there were 8-lb. of mass in excess, or in opposition to attraction.
If
now I am splitting hairs, it is only to drive a point, for the attraction
between two bodies is not the product of their masses. But
rather, the attraction between two bodies is the product of their magnetic and gravitational force in the interaction thereof, which again is relative to the movements of the masses.
We saw how the gravitational attraction of the moon was much greater for its mass relevant to that of the earth on a person standing thereon. If that is not sufficient evidence to discard Newton’s theory, and every other current theory, how much light do we require?
Let
us entertain F=Gm1 x m2/r2,
and take Henry at 165-lb. on the surface of the earth with Carl at 165-lb. some
200 miles above the earth. As then
the distance is 1056000-ft, and g at
32.14 + 31.34 : 2 = 31.74-ft/sec
Or,
the satellite in which Carl is having his vacation,
Is there then really almost one pound of attraction between Henry and Carl, when it is experimentally and mathematically indisputable that there is a gravitational attraction upon Carl of 5186-lb?
And what if Carl decides to put all of us in the wrong by a little blast of his jets to depart, as in opposite to attraction - to recede? How will we say; there is 0.82-lb of attraction between us, when he is waving good-by to us?
If I tell a young lady that I have a 100% attraction for her, and she walks off, what does that do to my attraction? Obviously it was not very real but merely a misconception on my part.
Or what will it do to the satellite if in its assumed stable orbit it still has a weight of 270.5-lb. of attraction to mother earth? If indeed the 270.5-lb were the g force still on it, it would not remain in orbit.
And still assuming the 270.5-lb to be a correct measure of gravitational attraction, then how do we account for the inertia of its velocity? Is there no reaction to it? And if there is, where is that written or accounted for? And how or where does its weight, its gravitational or spring weight fit in?
Am I going to win this argument or are we such that we will not surrender
our fallacies as our values? Would that the matter of attraction between celestial bodies
be as simple as just measuring the gravitational data between them.
But everything in nature is “twofold,” there is right and wrong, good and bad, up or down, right or left, even man is twofold, as is force and motion, and the phenomena of celestial attraction no less twofold.
There is then a “cause” as also the “entity” to the phenomena of attraction. The cause is first of all “motion”, the movement of matter, while the foremost entity is magnetism, the force known as magnetic, which should not be too difficult since we have seen how magnets are drawn to one another by and in their direction of force (their polarities). The celestial bodies then are just a bit larger with their tentacles of force covering great distances.
Second in the twofold phenomena of attraction is gravity as a product by and of movement within a magnetic field - as seemingly a force, but in reality no more than an inclination towards a direction of.
When therefore I said “movement within” there is no exclusion, but the same includes inertia as it does circular velocity, or acceleration. It is after all by magnetic force that the earth is kept at a constant orbital velocity and in its daily rotation to maintain a constant thereof.
Granted
it is primarily gravity whereby objects are held to a planet, but the main force
to the attraction between celestial bodies lies with magnetic interaction, to
which the tides upon the earth are perfect evidence. These things, strange, or as new as they may be to us, are
part of the second part of this report.
Meanwhile, to calculate the force of attraction on celestial bodies by a magnetic constant, I do not believe there is a universal constant, but each star or planet may be given its own, with the attraction between them in the inverse proportion between them.
Nor shall this be simple since here we must consider the stars and planets in their polarities as well as nearby celestial bodies, in addition to the gravitational inclination that each of these magnetic bodies pose in the twofold attraction.
CONCLUSION
Conclusively, it is a fallacy to think that we have it all figured out so simply, seeing how there is much more in Santa’s bag than what appeared unto the eye. Not that I have all the answers, but it lies within common sense and logical deduction to interpret everyday experience for their meaning.
How will it be denied that the atom with its electrons in circular movement, producing a velocity to give light its great speed, not to give mass its inertia? And if gravity does not act upon this inertia, why are we placing that momentum of gravity in its acceleration to causes which are not of gravity, such as the acceleration of a vehicle in a horizontal plane?
And
why is it that the rate of the acceleration of gravity is not used when finding
the force of the inertia by velocity in a circular path, and yet it is equally a
value of the force of gravity? Or,
if gravity is just some universal wave, why does the gravity of the different
planets and of the stars vary in strength and rate of velocity?
Coming back to the atom in our illustration figure 28-1, item 8, what is the only real impact we can place upon this gyro to produce a movement other than its existing angular inertia? A movement of precession, is the only answer to this, by a torque placed upon it.
From our inertial guidance systems we know that any change in movement or direction thereof will cause this movement of precession, which again is a momentum equal to the torque in the force of the angular. It is this movement of precession in the force behind it that is rightfully called “the inclination of gravity".
This
inclination then is just as it states - to incline into. And
what it inclines into is the very same force which initiated its direction of
precession as in - by in large placing the torque, that then may be increased by
a cause other than magnetic, i.e. movement (velocity and change in direction of
movement).
Consequently, I am correct in grafting upon the illustration that the direction to which gravitational pull is directed is not one of gravity, nor in the gyro, nor in the inertia, but of the magnetic force of the earth, the one and only force with a true center of.
How strange then shall it be for the atomic gyro’s to have a precession forged upon them and yet are not seen to be moving in their mass like the wobbling of a top, when our bodies are likewise at all times at an acceleration of 32 ft/sec, and yet we are not moving as such?
THE SCENARIO TO GRAVITATIONAL INCLINATION
Magnetic force, in its far-reaching wavelength, which at all times embraces all of the mass provides the initiative if not the primary torque as well upon the atomic gyro (Figure 28-1) from 10 by 6 to 8). Additional torque, if not all torque, comes from movement, from the linear velocity into the change in direction, wherefore I placed an arrow (number 7) from the axis pointing to “CAUSE = VELOCITY”
What therefore is written between the lines is, that without movement into a change of direction, there cannot be gravity, since without it there is no torque. And without torque there is no precession, and without precession there is no turning in the embrace of the arms of magnetic force, which by its directive forged a direction of the precession towards its center of. And it is the same masculine power to motivate any and all mass.
And so unless I am mistaken in some part. It
should be correct, that without the movement of the earth to turn in orbit, and
to rotate on its axis there would be no gravitational inclination, even as
without angular inertia in the atomic mass there would be no movement for yet
another movement to place still another movements which in all respects becomes
the inclination of gravity. And if
there were no magnetic force, there would be no female of force to be made of
the male.
MATTER
IN MOTION
All physical nature is by “matter in motion". This simply cannot be denied in any rational terms. Nor is there any force but motion, for whatever may be named in terms of force or energy is none other than motion. It is by motion that the atom spins, and by that matter in motion whereby each of these link to one another, and so on to form the structures of all that may be seen by the eye.
And again their
movement in what we came to call inertia is what will kill men on his freeways. And
is it not also movement for the power in the twisters of the earth, and its
hurricanes?
“Matter in Motion by Coordination” as I called it in my resume, the book I was given to write divulging all of the fundamentals. What is acceleration if not matter in motion, and what is circular velocity, or inertia, or precession if not all the same?
Or a wave for that matter, or lines of force. Do we not attribute velocity, that is to say “motion” unto waves? And while a line of force (magnetic) may just be the longest of the waves with no more than a single twist in their formation, it nonetheless ranks as a wave.
For when we as humans take that wave and twist it like one twists a rubber band, we proudly acclaim to have discovered electricity, and marvel at the fact that there is magnetic force associated with it. Well, no wonder, if one grinds wheat into flower how will he say of the flower it is not akin to wheat?
But to dissect
the atom for an explanation of this simple phenomena is going a bit too far.
If then it is beyond men to comprehend the reality of something as simple as electricity, or of light in its nature of being - how will he come to hear concerning gravity which follows a scenario more difficult to follow?
I therefore shall be as one too far ahead of its time and in time as the day grows into age and the old depletes itself for the new, men will come to cherish the truth, and it will be for healing unto them.
